MATLAB: Thermal Systems

Q1: How does the cooling behavior change if we vary the parameters Rth and C?
C is the heat capacity of a liquid which is the amount of energy the can be applied before a temperature change occurs. So when C is increased, it takes a much longer time for the coffee cool down while when C is decreased, the coffee is able to cool down very quickly. Rth is the thermal resistance of  a substance. So when Rth is increased, the coffee cools down very slowly while when Rth is decreased, it cools down nearly instantly.

C = 1000 | Rth = 0.85

C = 5000 | Rth = 0.85

C = 100 | Rth = 0.85

C = 1000 | Rth = 10

C = 1000 | Rth = 0.01

Q2: Calculate a good value for P if we want our coffee to heat up to the Starbucks ideal of 84 degrees Celsius, using the Rth frm the MATLAB script.

(P/C) = (dT/dt) + ((T-Tair)/(Rth*C))
Because dT = 0 and dt = 0 initially we can simplify the equation to:
(P/C) = ((T-Tair)/(Rth*C))
The C on both sides cancel out and we are left with:
P = (T-Tair) / Rth
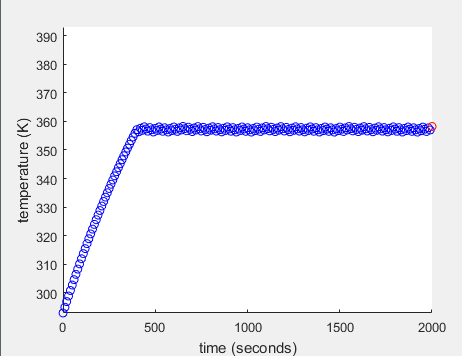
P = (357-293) / 0.85 = 64 / 0.85 = 75


Working Backwards: Can you dedeuce the thermal parameters C and Rth?
In order to find Rth, we use the equation:
P = (T-Tair) / Rth
Rth = delta T / P = 63 K / 75 W = 0.84 K/W

In order to find C, we can use the equation:
dT/dt = P/C
because at t=0, there is only energy flowing into the system.
SO we can rearrange the equation and get:
C = P / slope = (75 W) / (0.075 K/s) = 1000 J/K

Q3: Heat coffee using bang bang control
Bang bang control is appropriate for thermal systems because it is much simpler to just turn on and off a heater. It can be insufficient though because even with just a slight deviation from a target temperature a heater would immediately turn on or off causing a waste in energy.




Q4: Heat coffee using proportional control
With proportional control, we heat the coffee according to the amount it needed to go back to the ideal temperature and so the power did not always have to be at its maximum. The heat put into the system is proportional to the amount the temperature of the coffee deviated from the ideal 84 degrees.



Q5: Delay
Adding in a delay in bang bang control did not change the system very much. When the delay was larger than 10 though, we could see when the temperature would fluctuate from below ideal to ideal temperature.

delay 10 seconds

delay 25 seconds

Adding a delay in proportional control causes a huge difference in the very beginning. We can see that a large amount of heat was first added in the beginning since there was a large difference in the temperature of the coffee and the ideal temperature. Then as the temperature of the coffee got closer to the ideal, the heat added was more constant.